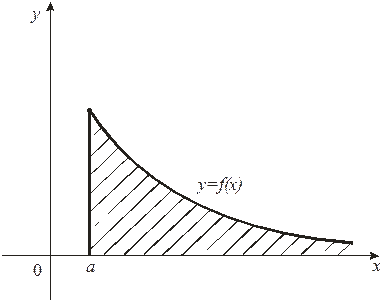
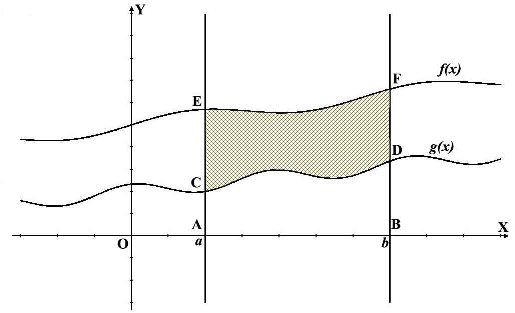
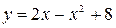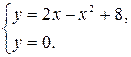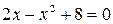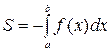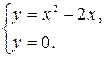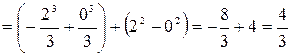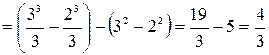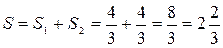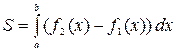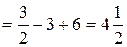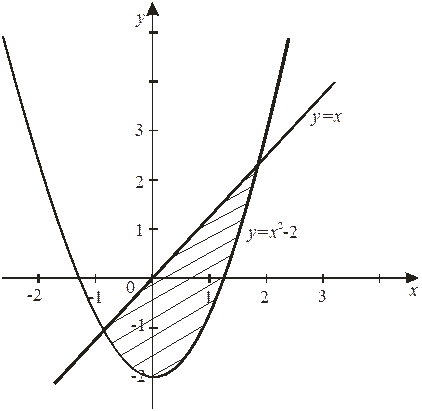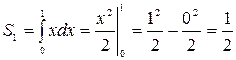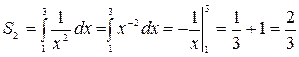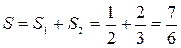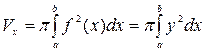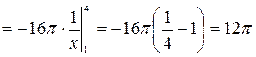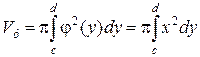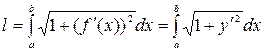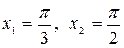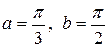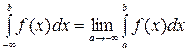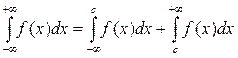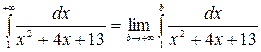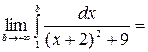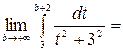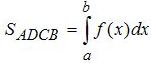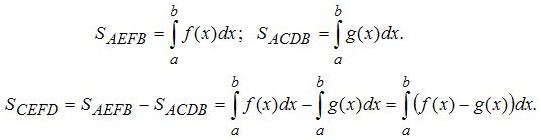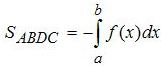У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. На уроке я говорил, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ
.
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры
. Например, рассмотрим определенный интеграл . Подынтегральная функция задает на плоскости некоторую кривую (её можно всегда при желании начертить), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.
Пример 1
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа
. Причем, чертеж необходимо построить ПРАВИЛЬНО
.
При построении чертежа я рекомендую следующий порядок: сначала
лучше построить все прямые (если они есть) и только потом
– параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно
, с техникой поточечного построения можно ознакомиться в справочном материале .
Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.
В данной задаче решение может выглядеть так.
Выполним чертеж (обратите внимание, что уравнение задает ось ):
Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. Решение продолжается так:
На отрезке график функции расположен над осью
, поэтому:
Ответ:
У кого возникли трудности с вычислением определенного интеграла и применением формулы Ньютона-Лейбница
, обратитесь к лекции
Определенный интеграл. Примеры решений
.
После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 2
Вычислить площадь фигуры, ограниченной линиями , , и осью
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Что делать, если криволинейная трапеция расположена под осью ?
Пример 3
Вычислить площадь фигуры, ограниченной линиями , и координатными осями.
Решение: Выполним чертеж:
Если криволинейная трапеция
полностью расположена под осью
, то её площадь можно найти по формуле:
В данном случае:
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому, от простейших школьных задачек переходим к более содержательным примерам.
Пример 4
Найти площадь плоской фигуры, ограниченной линиями , .
Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы и прямой . Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
Значит, нижний предел интегрирования , верхний предел интегрирования .
Этим способом лучше, по возможности, не пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Техника поточечного построения для различных графиков подробно рассмотрена в справкеГрафики и свойства элементарных функций
. Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). И такой пример, мы тоже рассмотрим.
Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:
Повторюсь, что при поточечном построении пределы интегрирования чаще всего выясняются «автоматом».
А теперь рабочая формула:
Если на отрезке некоторая непрерывная функция больше либо равна
некоторой непрерывной функции , то площадь соответствующей фигуры можно найти по формуле:
Здесь уже не надо думать, где расположена фигура – над осью или под осью, и, грубо говоря, важно, какой график ВЫШЕ
(относительно другого графика), а какой – НИЖЕ
.
В рассматриваемом примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из необходимо вычесть
Завершение решения может выглядеть так:
Искомая фигура ограничена параболой сверху и прямой снизу.
На отрезке , по соответствующей формуле:
Ответ:
На самом деле школьная формула для площади криволинейной трапеции в нижней полуплоскости (см. простенький пример №3) – частный случай формулы
. Поскольку ось задается уравнением , а график функции расположен ниже оси , то
А сейчас пара примеров для самостоятельного решения
Пример 5
Пример 6
Найти площадь фигуры, ограниченной линиями , .
В ходе решения задач на вычисление площади с помощью определенного интеграла иногда случается забавный казус. Чертеж выполнен правильно, расчеты – правильно, но по невнимательности… найдена площадь не той фигуры
, именно так несколько раз лажался ваш покорный слуга. Вот реальный случай из жизни:
Пример 7
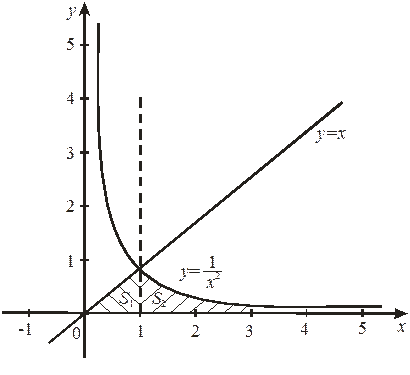
Вычислить площадь фигуры, ограниченной линиями , , , .
Сначала выполним чертеж:
Фигура, площадь которой нам нужно найти, заштрихована синим цветом
(внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает, что нужно найти площадь фигуры, которая заштрихована зеленым цветом!
Этот пример еще и полезен тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке над осью расположен график прямой ;
2) На отрезке над осью расположен график гиперболы .
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:
Ответ:
Пример 8
Вычислить площадь фигуры, ограниченной линиями ,
Представим уравнения в «школьном» виде , и выполним поточечный чертеж:
Из чертежа видно, что верхний предел у нас «хороший»: .
Но чему равен нижний предел?! Понятно, что это не целое число, но какое? Может быть ? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что . Или корень. А если мы вообще неправильно построили график?
В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.
Найдем точки пересечения прямой и параболы .
Для этого решаем уравнение:
Следовательно, .
Дальнейшее решение тривиально, главное, не запутаться в подстановках и знаках, вычисления здесь не самые простые.
На отрезке
, по соответствующей формуле:
Ну, и в заключение урока, рассмотрим два задания сложнее.
Пример 9
Вычислить площадь фигуры, ограниченной линиями , ,
Решение: Изобразим данную фигуру на чертеже.
Для поточечного построения чертежа необходимо знать внешний вид синусоиды (и вообще полезно знать графики всех элементарных функций
), а также некоторые значения синуса, их можно найти в тригонометрической таблице
. В ряде случаев (как в этом) допускается построение схематического чертежа, на котором принципиально правильно должны быть отображены графики и пределы интегрирования.
С пределами интегрирования здесь проблем нет, они следуют прямо из условия: – «икс» изменяется от нуля до «пи». Оформляем дальнейшее решение:
На отрезке график функции расположен над осью , поэтому:
(1) Как интегрируются синусы и косинусы в нечетных степенях можно посмотреть на урокеИнтегралы от тригонометрических функций
. Это типовой прием, отщипываем один синус.
(2) Используем основное тригонометрическое тождество в виде
(3) Проведем замену переменной , тогда:
Новые переделы интегрирования:
У кого совсем плохи дела с заменами, прошу пройти на урок Метод замены в неопределенном интеграле
. Кому не очень понятен алгоритм замены в определенном интеграле, посетите страницу Определенный интеграл. Примеры решений
.
Задача 1
(о вычислении площади криволинейной трапеции).
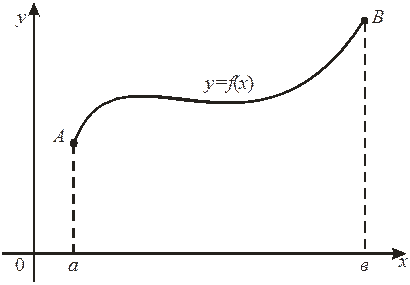
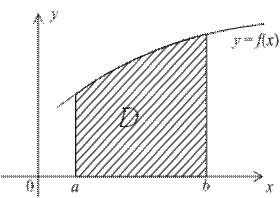
В декартовой прямоугольной системе координат xOy дана фигура (см. рисунок), ограниченная осью х, прямыми х = a, х = b (a криволинейной трапецией. Требуется
вычислить площадь криволинейной трапеции.
Решение.
Геометрия дает нам рецепты для вычисления площадей многоугольников и некоторых частей круга (сектора, сегмента). Используя
геометрические соображения, мы сумеем найти лишь приближенное значение искомой площади, рассуждая следующим образом.
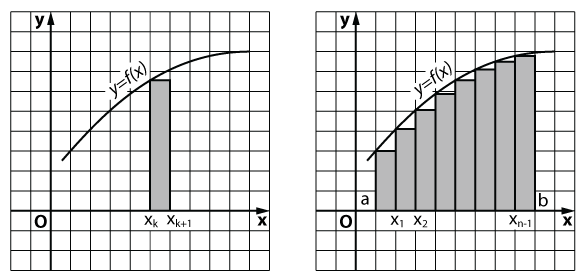
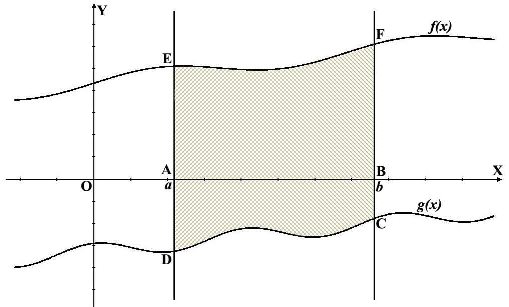
Разобьем отрезок [а; b] (основание криволинейной трапеции) на n равных частей; это разбиение осуществим с помощью точек x 1 ,
x 2 , … x k , … x n-1 . Проведем через эти точки прямые, параллельные оси у. Тогда заданная
криволинейная трапеция разобьется на n частей, на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.
Рассмотрим отдельно k-ый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок .
Заменим его прямоугольником с тем же основанием и высотой, равной f(x k) (см. рисунок). Площадь прямоугольника равна
(f(x_k) cdot Delta x_k ), где (Delta x_k ) – длина отрезка ; естественно
считать составленное произведение приближенным значением площади k-го столбика.
Если теперь сделать то же самое со всеми остальными столбиками, то придем к следующему результату: площадь S заданной криволинейной
трапеции приближенно равна площади S n ступенчатой фигуры, составленной из n прямоугольников (см. рисунок):
(S_n = f(x_0)Delta x_0 + dots + f(x_k)Delta x_k + dots + f(x_{n-1})Delta x_{n-1} )
Здесь ради единообразия обозначений мы считаем, что a = х 0 , b = x n ; (Delta x_0 ) – длина
отрезка ,
(Delta x_1 ) – длина отрезка , и т.д; при этом, как мы условились выше,
(Delta x_0 = dots = Delta x_{n-1} )
Итак, (S approx S_n ), причем это приближенное равенство тем точнее, чем больше n.
По определению полагают, что искомая площадь криволинейной трапеции равна пределу последовательности (S n):
$$ S = lim_{n to infty} S_n $$
Задача 2
(о перемещении точки)
По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t). Найти перемещение точки
за промежуток времени [а; b].
Решение.
Если бы движение было равномерным, то задача решалась бы очень просто: s = vt, т.е. s = v(b-а). Для неравномерного движения
приходится использовать те же идеи, на которых было основано решение предыдущей задачи.
1) Разделим промежуток времени [а; b] на n равных частей.
2) Рассмотрим промежуток времени и будем считать, что в этот промежуток времени скорость была
постоянной, такой, как в момент времени t k . Итак, мы считаем, что v = v(t k).
3) Найдем приближенное значение перемещения точки за промежуток времени , это приближенное
значение обозначим s k
(s_k = v(t_k) Delta t_k )
4) Найдем приближенное значение перемещения s:
(s approx S_n ) где
(S_n = s_0 + dots + s_{n-1} = v(t_0)Delta t_0 + dots + v(t_{n-1}) Delta t_{n-1} )
5) Искомое перемещение равно пределу последовательности (S n):
$$ s = lim_{n to infty} S_n $$
Подведем итоги. Решения различных задач свелись к одной и той же математической модели. Многие задачи из различных областей
науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить.
Понятие определенного интеграла
Дадим математическое описание той модели, которая была построена в трех рассмотренных задачах для функции y = f(x),
непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а; b]:
1) разбиваем отрезок [а; b] на n равных частей;
2) составляем сумму $$ S_n = f(x_0)Delta x_0 + f(x_1)Delta x_1 + dots + f(x_{n-1})Delta x_{n-1} $$
3) вычисляем $$ lim_{n to infty} S_n $$
В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует.
Его называют определенным интегралом от функции y = f(x) по отрезку [а; b]
и обозначают так:
(intlimits_a^b f(x) dx )
Числа a и b называют пределами интегрирования (соответственно нижним и верхним).
Вернемся к рассмотренным выше задачам. Определение площади, данное в задаче 1, теперь можно переписать следующим образом:
(S = intlimits_a^b f(x) dx )
здесь S – площадь криволинейной трапеции, изображенной на рисунке выше. В этом состоит геометрический смысл определенного интеграла.
Определение перемещения s точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t = a до t = b, данное
в задаче 2, можно переписать так:
Формула Ньютона – Лейбница
Для начала ответим на вопрос: какая связь между определенным интегралом и первообразной?
Ответ можно найти в задаче 2. С одной стороны, перемещение s точки, движущейся по прямой со скоростью v = v(t), за промежуток
времени от t = а до t = b и вычисляется по формуле
(S = intlimits_a^b v(t) dt )
С другой стороны, координата движущейся точки есть первообразная для скорости – обозначим ее s(t); значит, перемещение s
выражается формулой s = s(b) – s(a). В итоге получаем:
(S = intlimits_a^b v(t) dt = s(b)-s(a) )
где s(t) – первообразная для v(t).
В курсе математического анализа доказана следующая теорема.
Теорема. Если функция y = f(x) непрерывна на отрезке [а; b], то справедлива формула
(S = intlimits_a^b f(x) dx = F(b)-F(a) )
где F(x) – первообразная для f(x).
Приведенную формулу обычно называют формулой Ньютона – Лейбница
в честь английского физика Исаака Ньютона (1643-1727)
и немецкого философа Готфрида Лейбница (1646- 1716), получивших ее независимо друг от друга и практически одновременно.
На практике вместо записи F(b) – F(a) используют запись (left. F(x)right|_a^b )
(ее называют иногда двойной подстановкой
) и, соответственно, переписывают формулу Ньютона – Лейбница в таком виде:
(S = intlimits_a^b f(x) dx = left. F(x)right|_a^b )
Вычисляя определенный интеграл, сначала находят первообразную, а затем осуществляют двойную подстановку.
Опираясь на формулу Ньютона – Лейбница, можно получить два свойства определенного интеграла.
Свойство 1.
Интеграл от суммы функций равен сумме интегралов:
(intlimits_a^b (f(x) + g(x))dx = intlimits_a^b f(x)dx + intlimits_a^b g(x)dx )
Свойство 2.
Постоянный множитель можно вынести за знак интеграла:
(intlimits_a^b kf(x)dx = k intlimits_a^b f(x)dx )
Вычисление площадей плоских фигур с помощью определенного интеграла
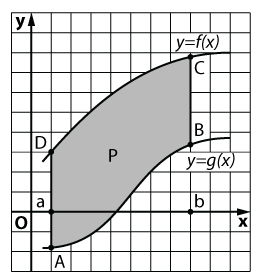
С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских
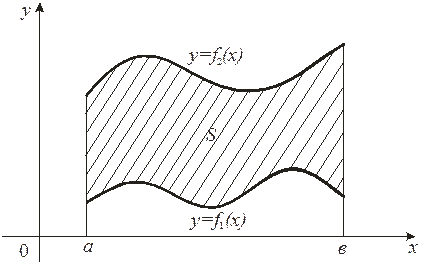
фигур более сложного вида, например такого, который представлен на рисунке. Фигура Р ограничена прямыми х = а, х = b и графиками
непрерывных функций y = f(x), y = g(x), причем на отрезке [а; b] выполняется неравенство (g(x) leq f(x) ). Чтобы вычислить
площадь S такой фигуры, будем действовать следующим образом:
(S = S_{ABCD} = S_{aDCb} – S_{aABb} = intlimits_a^b f(x) dx – intlimits_a^b g(x) dx = )
(= intlimits_a^b (f(x)-g(x))dx )
Итак, площадь S фигуры, ограниченной прямыми х = а, х = b и графиками функций y = f(x), y = g(x), непрерывных на отрезке
и таких, что для любого x из отрезка [а; b] выполняется неравенство (g(x) leq f(x) ), вычисляется по формуле
(S = intlimits_a^b (f(x)-g(x))dx )
Таблица неопределённых интегралов (первообразных) некоторых функций
$$ int 0 cdot dx = C $$
$$ int 1 cdot dx = x+C $$
$$ int x^n dx = frac{x^{n+1}}{n+1} +C ;; (n neq -1) $$
$$ int frac{1}{x} dx = ln |x| +C $$
$$ int e^x dx = e^x +C $$
$$ int a^x dx = frac{a^x}{ln a} +C ;; (a>0, ;; a neq 1) $$
$$ int cos x dx = sin x +C $$
$$ int sin x dx = -cos x +C $$
$$ int frac{dx}{cos^2 x} = text{tg} x +C $$
$$ int frac{dx}{sin^2 x} = -text{ctg} x +C $$
$$ int frac{dx}{sqrt{1-x^2}} = text{arcsin} x +C $$
$$ int frac{dx}{1+x^2} = text{arctg} x +C $$
$$ int text{ch} x dx = text{sh} x +C $$
$$ int text{sh} x dx = text{ch} x +C $$
Пусть функция неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле
Пример 9.
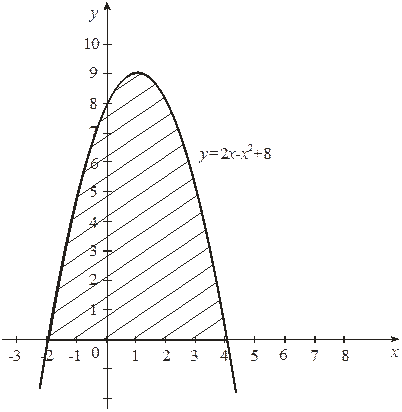
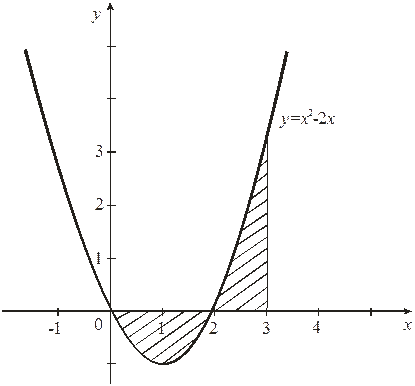
Найти площадь фигуры, ограниченной линией и осью .
Решение
. Графиком функции
является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений
Получаем:
, откуда , ; следовательно, , .
Рис. 3
Площадь фигуры находим по формуле (5):
Если функция неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле
. (6)
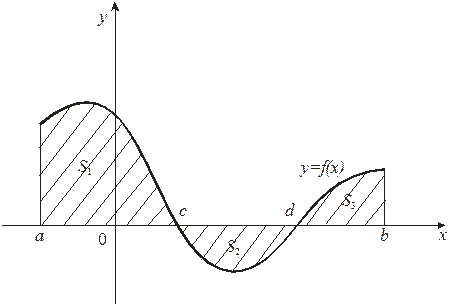
В случае, если функция непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
Рис. 4
Пример 10.
Вычислить площадь фигуры, ограниченной осью и графиком функции при .
Рис. 5
Решение
. Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему
Получим , . Следовательно:
;
.
Таким образом, площадь заштрихованной фигуры равна
(кв. ед.).
Рис. 6
Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке функций и ,
а слева и справа – прямыми и (рис. 6). Тогда ее площадь вычисляется по формуле
. (8)
Пример 11.
Найти площадь фигуры, ограниченной линиями и .
Решение.
Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений находим , ; следовательно, , . На отрезке имеем: . Значит, в формуле (8) в качестве возьмем x
, а в качестве – . Получим:
(кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
Рис. 7
Пример 12.
Найти площадь фигуры, ограниченной линиями , , .
Решение
. Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью , слева и справа – прямыми и , сверху – графиками функций и . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой на две части (1 – это абсцисса точки пересечения линий и ). Площадь каждой из этих частей находим по формуле (4):
(кв. ед.);
(кв. ед.). Следовательно:
(кв. ед.).
Рис. 8
Рис. 9
В заключение отметим, что если криволинейная трапеция ограничена прямыми и , осью и непрерывной на кривой (рис. 9), то ее площадь находится по формуле
Объем тела вращения
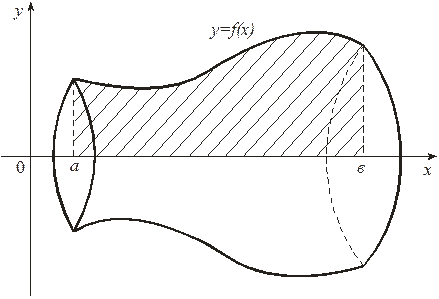
Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле
. (9)
Пример 13.
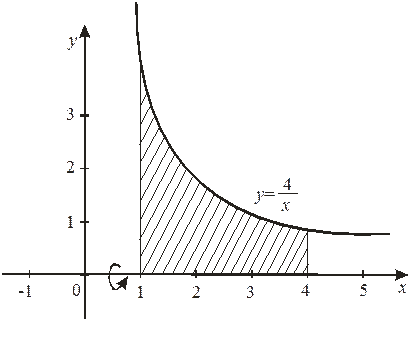
Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .
Решение
. Сделаем чертеж (рис. 11).
Из условия задачи следует, что , . По формуле (9) получаем
.
Рис. 10
Рис. 11
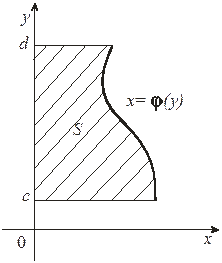
Объем тела, полученного вращением вокруг оси Оу
криволинейной трапеции, ограниченной прямыми у = с
и у = d
, осью Оу
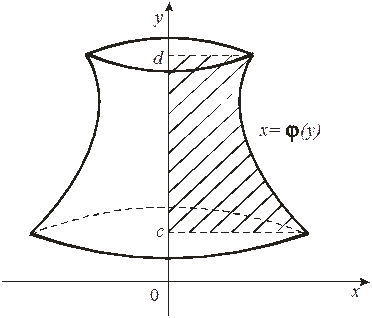
и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле
. (10)
Рис. 12
Пример 14
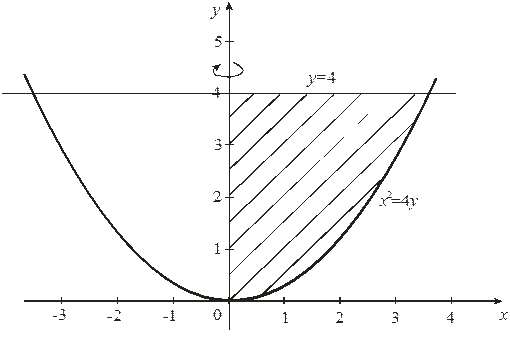
. Вычислить объем тела, полученного вращением вокруг оси Оу
криволинейной трапеции, ограниченной линиями х
2 = 4у
, у =
4, х =
0 (рис. 13).
Решение
. В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:
Рис. 13
Длина дуги плоской кривой
Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).
Рис. 14
Определение.
Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле
. (11)
Пример 15
. Вычислить длину дуги кривой , заключенной между точками, для которых
.
Решение
. Из условия задачи имеем
. По формуле (11) получаем:
4. Несобственные интегралы
с бесконечными пределами интегрирования
При введении понятия определённого интеграла предполага-лось, что выполняются следующие два условия:
а) пределы интегрирования а
и являются конечными;
б) подынтегральная функция ограничена на отрезке .
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным
.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение.
Пусть функция определена и непрерывна на промежутке , тогда
и неограниченной справа (рис. 15).
Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.
Рис. 15
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
. (13)
Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
, (14)
где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
;
г)
= [выделим в знаменателе полный квадрат: ] =
[замена:
] =
Значит, несобственный интеграл сходится и его значение равно .
Тема: Вычисление площади плоской фигуры с помощью определенного интеграла
Задачи: выучить определение и формулы нахождения площади криволинейной трапеции;
рассмотреть различные случаи нахождения площади криволинейной трапеции;
Уметь вычислять площадь криволинейной трапеции.
План:
Криволинейная трапеция.
Формулы вычисления площади криволинейной трапеции.
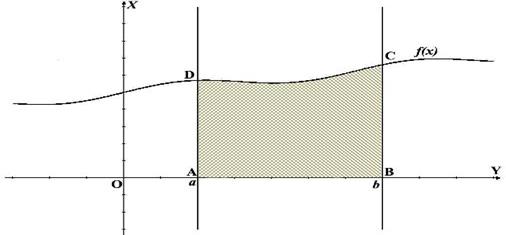
Криволинейной трапецией
называется фигура, которая ограничена графиком непрерывной, неотрицательной функции f(x) на промежутке , отрезками прямых x=a и x=b, а также отрезком оси абсцисс между точками a и b.
Изображения криволинейных трапеций:
Теперь перейдём к возможным вариантам расположения фигур, площадь которых надо вычислить на координатной плоскости.
Первым
будет самый простой вариант (первый рисунок), обычная
криволинейная трапеция
, как в определении. Здесь ничего не надо придумывать просто берём интеграл от
a
до
b
от функции
f(x)
. Найдём интеграл – будем знать и площадь данной трапеции.
Во
втором
варианте наша фигура будет ограничена не осью абсцисс, а другой функцией
g(x)
. Поэтому, что бы найти площадь
CEFD
, нам надо сначала найти площадь
AEFB
(с помощью интеграла от
f(x)
), потом найти площадь
ACDB
(с помощью интеграла от
g(x)
). И искомая площадь фигуры
CEFD
, будет разница между первой и второй площадями криволинейной трапеции. Поскольку границы интегрирования здесь одинаковые, то это всё можно записать под одним интегралом (смотрите формулы под рисунком) всё зависит от сложности функций, в каком случае проще будет найти интеграл.
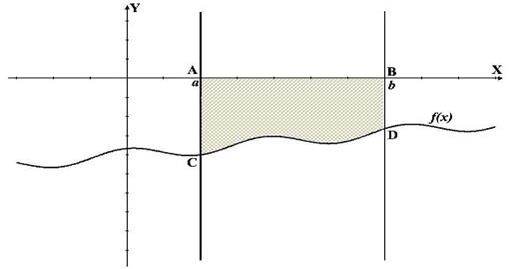
Третий
очень похож к первому, но только наша трапеция размещена, не над
осью абсцисс
, а под ней. Поэтому здесь надо брать такой же интеграл, только со знаком минус, потому что значение интеграла будет отрицательным, а значение площади должно быть положительное. Если вместо функции
f(x)
взять функцию
–f(x)
, то её график будет такой же просто симметрически отображен относительно оси абсцисс.
И
четвёртый
вариант, когда часть нашей фигуры находится над осью абсцисс, а часть под ней. Поэтому нам надо сначала найти площадь фигуры
AEFB
, как в первом варианте, а потом площадь фигуры
ABCD
, как в третьем варианте и потом сложить их. В итоге мы получим площадь фигуры
DEFC
. Поскольку границы интегрирования здесь одинаковые, то это всё можно записать под одним интегралом (смотрите формулы под рисунком) всё зависит от сложности функций, в каком случае проще будет найти интеграл.
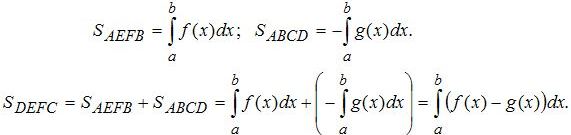
Вопросы для самопроверки:
Какая фигура называется криволинейной трапецией?
Как найти площадь криволинейной трапеции?